



Next: About this document ...
Up: Differential Geometry. Honours 1996
Previous: Vector fields and derivations.
Contents
If  and
and 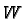 are finite dimensional vector spaces then
the Cartesian product
are finite dimensional vector spaces then
the Cartesian product
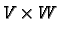 is naturally a
vector space called the direct sum of
is naturally a
vector space called the direct sum of  and
and 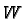 and
denoted
and
denoted 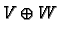 . The tensor product is a more complicated
object. To define it we start by defining for any set
. The tensor product is a more complicated
object. To define it we start by defining for any set
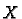 the free vector space over
the free vector space over 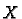 ,
, 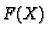 . This is the
set of all maps from
. This is the
set of all maps from 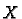 to
to
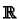 which are zero except at
a finite number of points. We define
the vector space structure by adding and scalar multiplying
maps. Each
which are zero except at
a finite number of points. We define
the vector space structure by adding and scalar multiplying
maps. Each 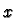 gives rise to a function
gives rise to a function
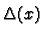 which is one at
which is one at 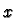 and zero elsewhere.
We therefore have a map
and zero elsewhere.
We therefore have a map
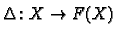 .
By construction the span of the image of
.
By construction the span of the image of 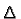 is all of
is all of
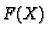 .
.
The special property of the free vector space over
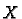 is the following.
is the following.
Proposition D.1
Let
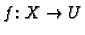
be any map from
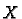
into a vector space
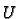
then there is a unique
linear map
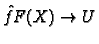
such that
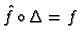
.
Proof.
The general element of
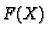
is
for
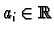
. We define

Given two vector spaces  and
and 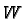 we can define
we can define
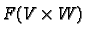 . This is an infinite dimensional
vector space. We shall denote
. This is an infinite dimensional
vector space. We shall denote
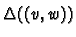 by
by
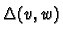 .
Consider the subspace
.
Consider the subspace 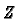 defined
as the span of all elements of the form
defined
as the span of all elements of the form
and
for any real numbers 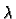 and
and 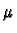 and vectors
and vectors
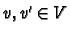 and
and
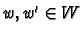 .
Let us denote
and define a map
by
We have
.
Let us denote
and define a map
by
We have
Proposition D.2
The map
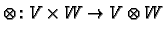
is bilinear.
Proof.
We check the first factor only

From Proposition D.1 we know that any map
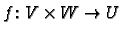 , where
, where 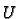 is a vector
space extends to a map
is a vector
space extends to a map
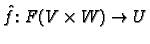 .
Standard linear algebra tells us that we can take
the quotient to get a map
.
Standard linear algebra tells us that we can take
the quotient to get a map
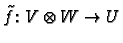 if
if
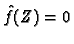 . The map is defined by
. The map is defined by
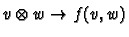 .
For example if
.
For example if
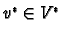 and
and
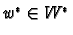 then
then
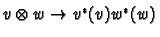 defines a linear map from
defines a linear map from
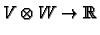 .
.
Let
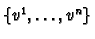 be a basis of
be a basis of  and
and
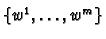 be a basis of
be a basis of 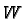 .
Consider the set of
.
Consider the set of 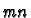 vectors
vectors
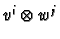 in
in
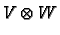 . We wish to show that they form a
basis. First we check that they span the space
. We wish to show that they form a
basis. First we check that they span the space
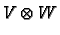 . As the elements of
. As the elements of
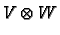 are
finite linear combinations of elements of the form
are
finite linear combinations of elements of the form
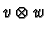 it suffices to show that these are all in the span of the
vectors
it suffices to show that these are all in the span of the
vectors
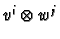 . But this follows from
the bilinearity. If
. But this follows from
the bilinearity. If
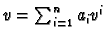 and
and
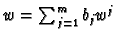 then
then
To show that they are linearly independent assume that
Let 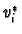 and
and 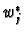 be the dual bases of
be the dual bases of 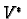 and
and 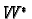 .
That is
.
That is
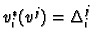 and
and
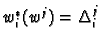 .
Then apply the map
.
Then apply the map
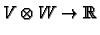 defined by
defined by 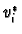 and
and
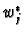 to this equation to obtain
to this equation to obtain
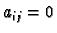 .
So we have proved.
.
So we have proved.
Proposition D.3
If

and
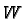
are finite dimensional
vector spaces then
We can iterate tensor products. If  and
and 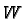 and
and 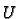 are vector spaces we can form
are vector spaces we can form
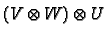 and
and
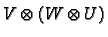 . These different vector
spaces are in fact isomorphic via the map
. These different vector
spaces are in fact isomorphic via the map
We use this map to identify these two spaces and ignore the
brackets. We write
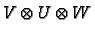 for
the triple tensor product. More generally we can form
finitely many tensor products.
for
the triple tensor product. More generally we can form
finitely many tensor products.
We also need to know about tensor products of maps. If
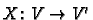 is linear and
is linear and
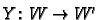 is
linear then we can define a map
is
linear then we can define a map
by
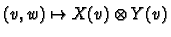 . This is a bilinear
map so factors to a map
. This is a bilinear
map so factors to a map
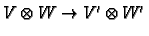 which we denote by
which we denote by
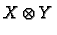 . It is defined by
. It is defined by
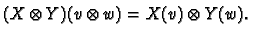
We have seen that any bilinear map
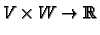 gives rise to a linear map
gives rise to a linear map
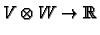 . It
is easy to show that this is an isomorphism. More
generally if for any collection of vector spaces
. It
is easy to show that this is an isomorphism. More
generally if for any collection of vector spaces
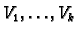 we denote by
Mult
we denote by
Mult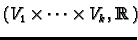 the
space of all multilinear maps from
the
space of all multilinear maps from
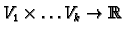 we have
we have
Proposition D.4
If
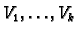
are vectors spaces then
there is a natural isomorphism
defined by




Next: About this document ...
Up: Differential Geometry. Honours 1996
Previous: Vector fields and derivations.
Contents
Michael Murray
1998-09-16
![]() is the following.
is the following.
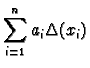
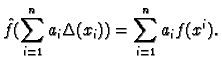
![]() and
and ![]() we can define
we can define
![]() . This is an infinite dimensional
vector space. We shall denote
. This is an infinite dimensional
vector space. We shall denote
![]() by
by
![]() .
Consider the subspace
.
Consider the subspace ![]() defined
as the span of all elements of the form
defined
as the span of all elements of the form
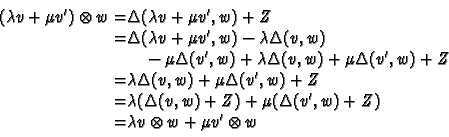
![]() , where
, where ![]() is a vector
space extends to a map
is a vector
space extends to a map
![]() .
Standard linear algebra tells us that we can take
the quotient to get a map
.
Standard linear algebra tells us that we can take
the quotient to get a map
![]() if
if
![]() . The map is defined by
. The map is defined by
![]() .
For example if
.
For example if
![]() and
and
![]() then
then
![]() defines a linear map from
defines a linear map from
![]() .
.
![]() be a basis of
be a basis of ![]() and
and
![]() be a basis of
be a basis of ![]() .
Consider the set of
.
Consider the set of ![]() vectors
vectors
![]() in
in
![]() . We wish to show that they form a
basis. First we check that they span the space
. We wish to show that they form a
basis. First we check that they span the space
![]() . As the elements of
. As the elements of
![]() are
finite linear combinations of elements of the form
are
finite linear combinations of elements of the form
![]() it suffices to show that these are all in the span of the
vectors
it suffices to show that these are all in the span of the
vectors
![]() . But this follows from
the bilinearity. If
. But this follows from
the bilinearity. If
![]() and
and
![]() then
then
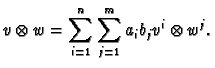
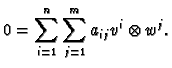
![]() and
and ![]() and
and ![]() are vector spaces we can form
are vector spaces we can form
![]() and
and
![]() . These different vector
spaces are in fact isomorphic via the map
. These different vector
spaces are in fact isomorphic via the map
![]() is linear and
is linear and
![]() is
linear then we can define a map
is
linear then we can define a map
![]() gives rise to a linear map
gives rise to a linear map
![]() . It
is easy to show that this is an isomorphism. More
generally if for any collection of vector spaces
. It
is easy to show that this is an isomorphism. More
generally if for any collection of vector spaces
![]() we denote by
Mult
we denote by
Mult![]() the
space of all multilinear maps from
the
space of all multilinear maps from
![]() we have
we have