Vector fields and derivations.

Let us now define derivations of $C^\infty(M)$.

Definition C.1   A derivation of $C^\infty(M)$ is a linear map

$$D \colon C^\infty(M) \to C^\infty(M)$$

such that

$$D(fg) = D(f) g + f D(g).$$

A vector field $X$ gives rise to a derivation $f \mapsto X(f)$ and using the previous Lemma we have

Proposition C.1   Every derivation arises from a vector field.

Proof. Let $D$ be a derivation. Then note that for any $x$ $f \mapsto D(f)(x)$ is a derivation at $x$. Hence there is a tangent vector $X(x)$ such that $D(f)(x) = X(x)(f)$ for all $x$. We have to check that $X(x)$ depends smoothly on $x$. But if we choose local co-ordinates $\psi$ as in the proof above and extend them to global functions $\psi$ then we have

$$X(x) = \sum_{i=1}^n D(\psi^i)(x) {\frac{\partial\phantom{\psi^i}}{\psi^i}}(x)$$

but $D(\psi)$ is a smooth function so by ?? $X(x)$ is smooth. $\qedsymbol$

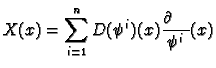
The advantage of thinking of a vector field as a derivation is that derivations have a natural bracket operation. If $D$ and $D'$ are two derivations then a simple calculation shows that $[D, D']$ defined by

$$[D, D'] (f) = D(D'(f)) - D'(D(f)).$$

is also a derivation. So we can define the bracket of two vector fields $X$ and $Y$ and called the Lie bracket $[X, Y]$. To calculate $[X, Y]$ we apply it to $\psi^i$ then we have

$$[X, Y](\psi^i) = X(Y(\psi^i)) - Y(X(\psi^i))$$

so that if

$$X = \sum_{i=1}^n X^i \frac{\partial\phantom{\psi^i}}{\psi^i}$$

and

$$Y = \sum_{i=1}^n Y^i \frac{\partial\phantom{\psi^i}}{\psi^i}$$

so that

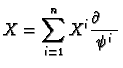
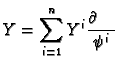
$$[X, Y](\psi^i) = \sum_{j=1}^n X^j\frac{\partial Y^i}{\partial \psi^j} - Y^j\frac{\partial X^i}{\partial \psi^j}.$$

Hence

$$[X, Y] = \sum_{i, j=1}^n (X^j\frac{\partial Y^i}{\partial \psi^j}... ...\frac{\partial X^i}{\partial \psi^j}) \frac{\partial\phantom{\psi^i}}{\psi^i}.$$