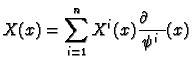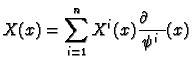Next: Vector fields and derivations.
Up: Differential Geometry. Honours 1996
Previous: Partitions of unity.
Contents
We have seen how to define tangent vectors
at a point of a manifold. In many problems we are interested
in vector fields, that is a choice of vector at every
point of a manifold. We can think of this in the following
manner. Take the union of all the tangent spaces, denote it by
and call it the tangent bundle to 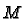 . There is an
important map
. There is an
important map
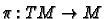 called the
projection that sends a vector
called the
projection that sends a vector
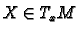 to the point
to the point 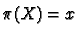 at which it is located. A vector
field is a map
at which it is located. A vector
field is a map
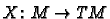 with the special property
that
with the special property
that
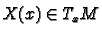 . This property can be
also written as
. This property can be
also written as
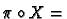 id
id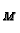 , that is
, that is
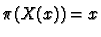 . Such a map
. Such a map
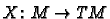 is called
a section of the projection map
is called
a section of the projection map 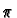 . We want to
consider smooth vector fields and as we already
have a notion of smooth function between manifolds
the simplest way to define smooth vector fields is to
make
. We want to
consider smooth vector fields and as we already
have a notion of smooth function between manifolds
the simplest way to define smooth vector fields is to
make 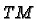 a manifold. To do this involves a construction
that we will use again later so we ill state it in
more general form that immediately necessary.
a manifold. To do this involves a construction
that we will use again later so we ill state it in
more general form that immediately necessary.
Let 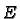 be a set with a surjection
be a set with a surjection
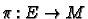 where
where
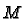 is a manifold. Denote by
is a manifold. Denote by 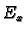 the fibre
of
the fibre
of 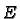 over
over 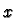 , that is the set
, that is the set
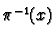 .
Let
.
Let  be a finite dimensional vector space. Assume that we
can cover
be a finite dimensional vector space. Assume that we
can cover 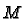 by co-ordinate charts
by co-ordinate charts
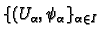 such that for
every
such that for
every
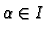 and for every
and for every
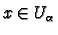 there is
a bijection
there is
a bijection
such that the map
is smooth where 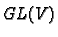 is the group
of all linear isomorphisms of
is the group
of all linear isomorphisms of  . Then it
is possible to make
. Then it
is possible to make 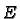 a manifold as follows. We define
bijections
To make these into charts we should really identify
a manifold as follows. We define
bijections
To make these into charts we should really identify
 with some
with some
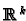 but we will not bother to
do that. To check compatibility we note that
but we will not bother to
do that. To check compatibility we note that
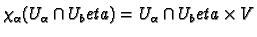 which is open in
which is open in
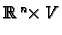 . Likewise
for
. Likewise
for
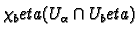 . Then the map
we want to check is smooth is the map
which sends
. Then the map
we want to check is smooth is the map
which sends 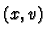 to
to
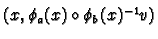 and this is smooth and invertible. By interchanging
and this is smooth and invertible. By interchanging
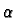 and
and 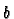 we deduce that this map is a diffeomorphism. Hence
we have made
we deduce that this map is a diffeomorphism. Hence
we have made 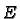 into a manifold. Notice that with this
manifold structure the map
into a manifold. Notice that with this
manifold structure the map
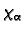 is a diffeomorphism,
as the co-ordinate charts of a manifold are diffeomorphisms.
Notice also that each
is a diffeomorphism,
as the co-ordinate charts of a manifold are diffeomorphisms.
Notice also that each 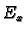 is a vector space from Lemma ??.
Moreover it easy to check that the addition and scalar
multiplication are smooth. Define a section of
is a vector space from Lemma ??.
Moreover it easy to check that the addition and scalar
multiplication are smooth. Define a section of
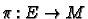 to be a smooth map
to be a smooth map
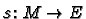 which satisfies
which satisfies
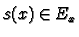 for all
for all 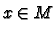 . If
. If 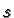 is such a section
then on restriction to
is such a section
then on restriction to 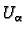 we can define a map
we can define a map
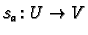 by
by
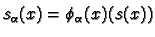 .
The
.
The 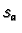 are clearly smooth. The converse is also
true if
are clearly smooth. The converse is also
true if 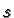 is any map and the
is any map and the 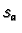 defined in this
way are smooth then
defined in this
way are smooth then 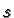 is smooth.
is smooth.
Consider now the case of the tangent bundle. Let
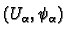 be a
co-ordinate chart on
be a
co-ordinate chart on 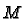 . Then
. Then
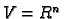 and
and
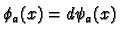 .
The condition we require to hold is that the
map
.
The condition we require to hold is that the
map
is smooth. But this is just the Jacobian matrix of partial derivatives which depends
smoothly on 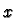 .
.
We can now define
Definition B.1
A smooth vector field on a manifold
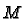
is a smooth section
of the tangent bundle.
To understand what it means to be smooth in
terms of co-ordinates recall the definition of
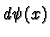 . We have the co-ordinate vector fields
. We have the co-ordinate vector fields
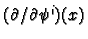 for
for
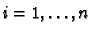 . Then
. Then
where 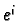 is the standard basis vector of
is the standard basis vector of
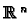 .
So clearly this is a smooth map so that the
co-ordinate vector fields are smooth.
.
So clearly this is a smooth map so that the
co-ordinate vector fields are smooth.
More generally if 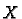 is a vector field
we can write it as
is a vector field
we can write it as
for any 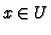 , and functions
, and functions
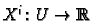 .
Then
This proves
.
Then
This proves
Proposition B.1
Let
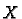
be a vector field on a manifold
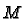
. Then if
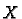
is
smooth and
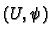
is a co-ordinate chart then if we let
the functions
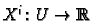
are smooth. Conversely
if
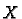
is a vector field and we can cover
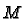
with
co-ordinate charts
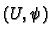
such that the corresponding
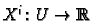
are smooth then
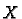
is smooth.




Next: Vector fields and derivations.
Up: Differential Geometry. Honours 1996
Previous: Partitions of unity.
Contents
Michael Murray
1998-09-16
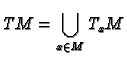
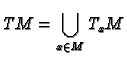
![]() be a set with a surjection
be a set with a surjection
![]() where
where
![]() is a manifold. Denote by
is a manifold. Denote by ![]() the fibre
of
the fibre
of ![]() over
over ![]() , that is the set
, that is the set
![]() .
Let
.
Let ![]() be a finite dimensional vector space. Assume that we
can cover
be a finite dimensional vector space. Assume that we
can cover ![]() by co-ordinate charts
by co-ordinate charts
![]() such that for
every
such that for
every
![]() and for every
and for every
![]() there is
a bijection
there is
a bijection
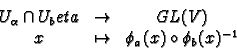
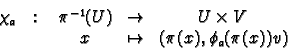
![]() be a
co-ordinate chart on
be a
co-ordinate chart on ![]() . Then
. Then
![]() and
and
![]() .
The condition we require to hold is that the
map
.
The condition we require to hold is that the
map
![]() . We have the co-ordinate vector fields
. We have the co-ordinate vector fields
![]() for
for
![]() . Then
. Then
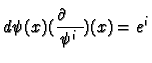
![]() is a vector field
we can write it as
is a vector field
we can write it as