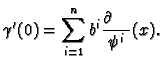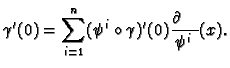Next: Submanifolds
Up: The tangent space.
Previous: Co-ordinate tangent vectors and
Contents
It is useful for calculations to know how
to expand various quantities in these
co-ordinate basis. First let 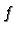 be a smooth
function on
be a smooth
function on 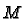 then we must have
for some real numbers
then we must have
for some real numbers 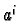 . This is just linear algebra
as is the fact that if we apply both sides of this equation
to
. This is just linear algebra
as is the fact that if we apply both sides of this equation
to
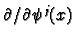 and use the dual basis relation we deduce
that
we define
and hence have the formula:
and use the dual basis relation we deduce
that
we define
and hence have the formula:
If 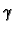 is a path through
is a path through 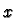 then its tangent
at 0,
then its tangent
at 0,
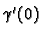 can be expanded as
can be expanded as
Applying
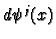 to both sides and
using the chain rule we deduce that
to both sides and
using the chain rule we deduce that
Michael Murray
1998-09-16
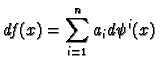
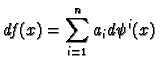
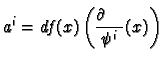
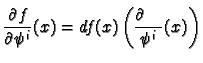
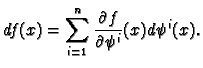
![]() is a path through
is a path through ![]() then its tangent
at 0,
then its tangent
at 0,
![]() can be expanded as
can be expanded as