



Next: Tangent space to a
Up: The tangent space.
Previous: How to calculate.
Contents
Historically the
theory of differential geometry arose from the study of
surfaces in
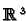 . We want to consider the more general
case of submanifolds in
. We want to consider the more general
case of submanifolds in
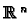 . Recall that we have
. Recall that we have
Definition 4.2
A set
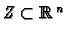
is a submanifold of dimension
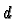
if
there is a smooth map
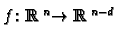
for some
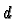
such that
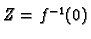
and
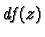
is onto for all
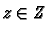
.
We will show that any submanifold of
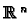 is a manifold
by constructing co-ordinate charts. The ideas is simple.
At any point
is a manifold
by constructing co-ordinate charts. The ideas is simple.
At any point 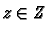 we define the plane tangent to
we define the plane tangent to
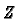 . This is the kernel
. This is the kernel 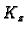 of the map
of the map 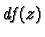 . Then we
consider orthogonal projection of
. Then we
consider orthogonal projection of 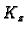 onto
onto 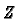 . This
defines co-ordinates on an open neighbourhood of
. This
defines co-ordinates on an open neighbourhood of 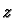 . In fact
these are a very special kind of co-ordinate. To prove this
we first prove
. In fact
these are a very special kind of co-ordinate. To prove this
we first prove
Proposition 4.2
Let
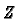
be a submanifold of
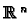
of dimension
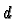
.
Then at any
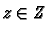
we can
find a co-ordinate chart
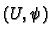
on
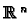
such that
if
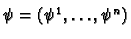
then
Proof.
Let
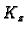
be the kernel of
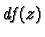
and let
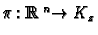
be the orthogonal projection onto
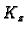
. Choose a basis
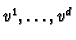
and write
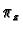
with respect to this basis as
Define a map
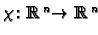
by
Because
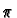
is a linear map it is its own derivative so
we have
Consider
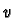
in the kernel of
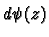
. Then
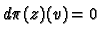
and
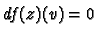
. Hence
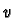
is both orthogonal to
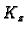
and in
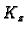
so it must be zero. So
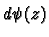
is injective
and hence a dimension count surjective so a bijection. Now
we can apply the inverse function theorem so there is an open
set
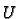
in
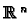
such that
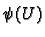
is open and
is a diffeomorphism. But this just means that
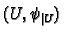
is a co-ordinate chart on
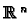
. Notice that
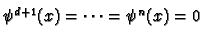
if and only if
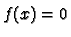
if and only
if
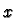
is in
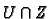
.

Let 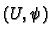 be a set of co-ordinates on
be a set of co-ordinates on
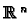 such that
such that
Then consider
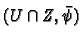 where
where
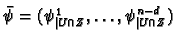 .
This is a co-ordinate chart. The only thing
to check is that that because
.
This is a co-ordinate chart. The only thing
to check is that that because 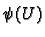 is open then
is open. This is an elementary fact about the topology of
is open then
is open. This is an elementary fact about the topology of
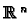 .
Consider two such co-ordinate charts
.
Consider two such co-ordinate charts 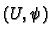 and
and
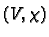 . We will prove that
. We will prove that
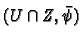 and
and
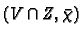 are compatible. This
follows essentially from the fact that
are compatible. This
follows essentially from the fact that 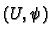 and
and 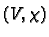 are compatible. First we note that
and, again, this is open. For the smoothness of the co-ordinate
change map we note that
where
are compatible. First we note that
and, again, this is open. For the smoothness of the co-ordinate
change map we note that
where
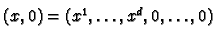 .
Hence the result follows.
.
Hence the result follows.
We have now proved
Theorem 4.1
If
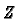
is a submanifold the set of charts above is
an atlas.
This results gives us a lot of examples of submanifolds:
Example 4.3 (Spheres)
Consider the sphere
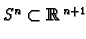
defined as the
set of points
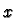
whose length
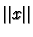
is equal to one. Here
We can prove it is a submanifold of
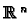
and hence a manifold
by considering the map
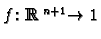
defined by
Clearly this is smooth and has zero set
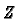
equal to the sphere
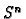
. To check that the derivative is smooth note that
and is a linear map onto a one-dimensional space so
to show it is onto we just need to show that it is not
equal to the zero linear maps.
Example 4.4 (The orthogonal group)
The orthogonal group is the group of all
linear transformations of
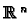
that preserve
the usual inner product on
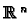
. We shall think of it as
a group of
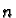
by
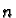
matrices:
We can identify the set of all
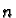
by
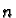
matrices
with
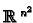
. There are various ways of doing this.
So as to be concrete let us assume we have done
it by writing down the rows one after the other.
With this identification in mind define a smooth
map
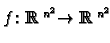
by
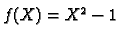
.
It is clear we have
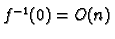
. Define the linear
subspace
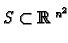
to be the set of all
symmetric matrices. This can be identified with
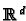
where
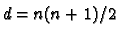
. It is easy to check that
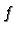
takes its values in
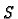
so we will think of
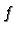
as a smooth map
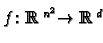
.
We want to calculate 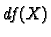 the derivative of
the derivative of 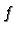 at a matrix
at a matrix 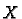 .
By differentiating the path
.
By differentiating the path
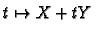 we obtain
we obtain
If
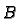
is any symmetric matrix then it is easy to
check that
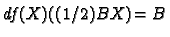
if we use that fact that
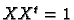
and
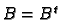
. We have therefore shown that
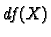
is onto for any
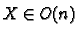
so that
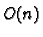
is a submanifold of dimension
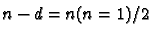
.




Next: Tangent space to a
Up: The tangent space.
Previous: How to calculate.
Contents
Michael Murray
1998-09-16
![]() is a manifold
by constructing co-ordinate charts. The ideas is simple.
At any point
is a manifold
by constructing co-ordinate charts. The ideas is simple.
At any point ![]() we define the plane tangent to
we define the plane tangent to
![]() . This is the kernel
. This is the kernel ![]() of the map
of the map ![]() . Then we
consider orthogonal projection of
. Then we
consider orthogonal projection of ![]() onto
onto ![]() . This
defines co-ordinates on an open neighbourhood of
. This
defines co-ordinates on an open neighbourhood of ![]() . In fact
these are a very special kind of co-ordinate. To prove this
we first prove
. In fact
these are a very special kind of co-ordinate. To prove this
we first prove
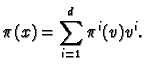
![]() be a set of co-ordinates on
be a set of co-ordinates on
![]() such that
such that
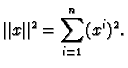
![]() the derivative of
the derivative of ![]() at a matrix
at a matrix ![]() .
By differentiating the path
.
By differentiating the path
![]() we obtain
we obtain