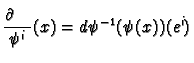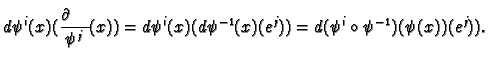Next: How to calculate.
Up: The tangent space.
Previous: The derivative of a
Contents
Let 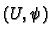 be a set of co-ordinates on
be a set of co-ordinates on 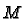 where
where
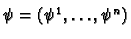 .
Then each of the component functions
.
Then each of the component functions 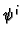 is a real function so we can define
is a real function so we can define 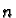 one-forms
one-forms
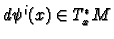 called the co-ordinate one-forms.
called the co-ordinate one-forms.
We have seen that
is a linear isomorphism. We denote by
the image under this map of the
standard basis vector 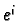 in
in
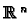 . We call the
set of these the basis of co-ordinate tangent vectors.
Consider what happens when we apply
. We call the
set of these the basis of co-ordinate tangent vectors.
Consider what happens when we apply
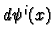 to
to
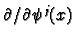 .
We have
Notice that if
.
We have
Notice that if
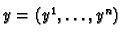 is a point
in
is a point
in
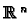 then
then
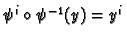 is a linear map so equal to its own derivative.
Hence
is a linear map so equal to its own derivative.
Hence
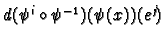 is the
is the
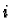 th component of the vector
th component of the vector 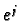 or just
or just
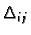 .
It follows from linear algebra that
.
It follows from linear algebra that
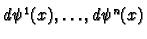 is a basis of
is a basis of 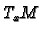 and, in fact, the dual basis to
the basis
and, in fact, the dual basis to
the basis
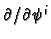 .
.
Michael Murray
1998-09-16