



Next: Smooth functions on a
Up: Differentiable manifolds
Previous: Linear manifolds.
Contents
Often a manifold is defined as a topological space
and the domains of the charts are required
to be open sets and the co-ordinates homeomorphisms.
This is really superfluous as the topology
is forced once we have chosen the atlas.
Given a manifold 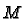 we define a subset
we define a subset
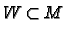 to be open if for every
to be open if for every 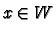 there is a chart
with domain
there is a chart
with domain 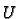 such that
such that
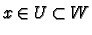 .
We need to show that such a definition of open
sets defines a topology on
.
We need to show that such a definition of open
sets defines a topology on 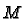 . The only problem
is showing that the intersection of two open sets is open.
This follows from the following Lemma whose proof we leave
as an exercise.
. The only problem
is showing that the intersection of two open sets is open.
This follows from the following Lemma whose proof we leave
as an exercise.
Lemma 2.1
Let
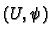
be a co-ordinate chart on a
manifold
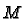
and let
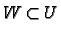
be such that
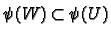
is open. Then
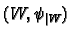
is a co-ordinate chart.
We also leave as an exercise showing that with this topology
if 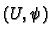 is a co-ordinate chart then
is a co-ordinate chart then
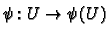 is a homeomorphism.
is a homeomorphism.
We will in general require a manifold to
be Hausdorff and paracompact in the topology.
Now that we have defined the topology of a manifold
we can discuss its dimension. Each co-ordinate function
has as range some
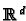 . From the definition of
compatibility it is clear that
. From the definition of
compatibility it is clear that 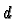 is constant on the
connected components of
is constant on the
connected components of 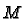 . We shall go further and
assume that our manifolds are such that this number
. We shall go further and
assume that our manifolds are such that this number
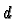 is constant on all of
is constant on all of  . We call it the
dimension of the manifold.
. We call it the
dimension of the manifold.




Next: Smooth functions on a
Up: Differentiable manifolds
Previous: Linear manifolds.
Contents
Michael Murray
1998-09-16
![]() is a co-ordinate chart then
is a co-ordinate chart then
![]() is a homeomorphism.
is a homeomorphism.
![]() . From the definition of
compatibility it is clear that
. From the definition of
compatibility it is clear that ![]() is constant on the
connected components of
is constant on the
connected components of ![]() . We shall go further and
assume that our manifolds are such that this number
. We shall go further and
assume that our manifolds are such that this number
![]() is constant on all of
is constant on all of ![]() . We call it the
dimension of the manifold.
. We call it the
dimension of the manifold.