



Next: Topology of a manifold
Up: Differentiable manifolds
Previous: Co-ordinate charts
Contents
There are many similarities between manifolds and
vector spaces. Choosing co-ordinates is much like choosing
a basis. It is useful to develop this idea further.
Definition 2.7
Define linear co-ordinates
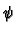
on a set

to be a bijection
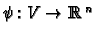
.
Definition 2.8
Define two sets of linear
co-ordinates
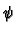
and
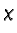
to be linearly equivalent if
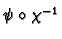
is a linear isomorphism.
It is straightforward to prove that linear equivalence
is an equivalence relation. We define
Definition 2.9
A linear atlas on a set

is an equivalence
class of linear co-ordinates.
Definition 2.10
We define a linear manifold to be a set

with a choice
of linear atlas.
We can define an addition and scalar multiplication
on  by choosing some linear co-ordinates
by choosing some linear co-ordinates 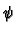 from the linear atlas and defining
from the linear atlas and defining
where 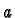 and
and 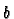 are real numbers and
are real numbers and 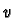 and
and
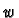 are elements of
are elements of  . We have to check that
this is well-defined that is it is independent
of the choice of
. We have to check that
this is well-defined that is it is independent
of the choice of 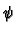 from the equivalence class.
If
from the equivalence class.
If 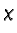 is another choice then we have
is another choice then we have
where in moving from the third to the fourth lines we use the
fact that
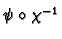 is linear.
We have proved.
is linear.
We have proved.
Proposition 2.2
A linear manifold has a natural vector space structure which
makes all of the linear co-ordinates linear isomorphisms.
Because of Proposition 2.2
the theory of linear manifolds is really the
theory of vector spaces. However it is an amusing
exercise to translate everything in the theory of
vector spaces into the linear manifold setting.
For example a function
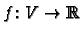 is linear if
is linear if
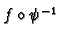 is linear some choice of
linear co-ordinates
is linear some choice of
linear co-ordinates 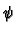 . It is then easy to
prove that
. It is then easy to
prove that
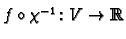 for any choice of linear co-ordinates
for any choice of linear co-ordinates 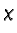 . Indeed
we just note that
. Indeed
we just note that




Next: Topology of a manifold
Up: Differentiable manifolds
Previous: Co-ordinate charts
Contents
Michael Murray
1998-09-16
![]() by choosing some linear co-ordinates
by choosing some linear co-ordinates ![]() from the linear atlas and defining
from the linear atlas and defining
![]() is linear if
is linear if
![]() is linear some choice of
linear co-ordinates
is linear some choice of
linear co-ordinates ![]() . It is then easy to
prove that
. It is then easy to
prove that
![]() for any choice of linear co-ordinates
for any choice of linear co-ordinates ![]() . Indeed
we just note that
. Indeed
we just note that