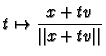Smooth functions on a manifold.

We motivated the definition of the compatibility of charts by the problem of defining smooth functions on a manifold. Let us do that now.

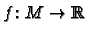
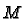
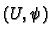
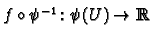
Definition 3.1   A function $f \colon M\to \mathbb{R}$ on a manifold $M$ is smooth if we can cover the manifold with co-ordinate charts $(U, \psi)$ such that $f \circ \psi^{-1} \colon \psi(U) \to \mathbb{R}$ is smooth.

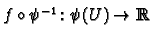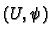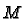Notice that we do not know that $f \circ \psi^{-1} \colon \psi(U) \to \mathbb{R}$ is smooth for any chart $(U, \psi)$ but only that we can cover $M$ with charts for which this is so. To get this stronger result we need the following Lemma.

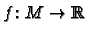
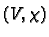
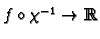
Lemma 3.1   If $f \colon M\to \mathbb{R}$ is a smooth function and $(V, \chi)$ is a co-ordinate chart then $f \circ \chi^{-1} \to \mathbb{R}$ is smooth.

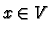
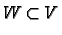
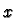
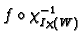
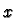
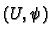
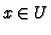
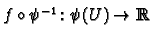
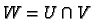
Proof. It suffices to show that for every $x\in V$ there is a $W \subset V$ containing $x$ such that $f \circ \chi^{-1}_{I\chi(W)}$ is smooth. Pick any such $x$. Then by definition there is a chart $(U, \psi)$ with $x \in U$ and $f \circ \psi^{-1} \colon \psi(U) \to \mathbb{R}$ smooth. Let $W = U \cap V$. Then

$$f \circ \chi^{-1}_{I\chi(W)} = (f \circ \psi^{-1}{I\psi(W)})\circ (\psi\circ \chi^{-1}{I\chi(W)})$$

which is smooth by the chain rule and compatibility of charts. $\qedsymbol$

We will also be interested in smooth functions into a manifold or paths. We have

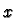
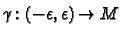
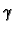
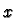
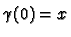
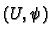
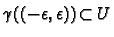
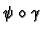
Definition 3.2   If $x$ is a point of a manifold and $\gamma \colon (-\epsilon, \epsilon) \to M$ we say that $\gamma$ is a smooth path through $x$ if $\gamma(0) = x$ and there is a chart $(U, \psi)$ with $\gamma((-\epsilon, \epsilon)) \subset U$ and such that $\psi\circ\gamma$ is smooth.

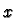
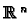
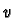
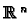
Example 3.1   If $x$ is a point in $\mathbb{R}^n$ and $v$ is a vector in $\mathbb{R}^n$ then the function

$$t \mapsto x + tv$$

is a curve through $x$.

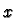
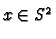
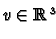
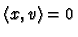
Example 3.2   If $x \in S^2$ and $v \in \mathbb{R}^3$ with $\< x, v\> = 0$ then

$$t \mapsto \frac{x + tv} { \Vert x+tv\Vert}$$

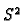
is a curve in $S^2$ through $x$.

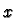
We have a similar type of lemma as before.

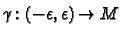
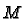
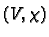
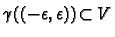
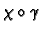
Lemma 3.2   If $\gamma \colon (-\epsilon, \epsilon) \to M$ is a smooth path in $M$ and $(V, \chi)$ is a chart with $\gamma ( (-\epsilon, \epsilon) ) \subset V$ then $\chi \circ \gamma$ is smooth.

Proof. Chain rule and compatibility. $\qedsymbol$