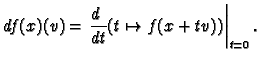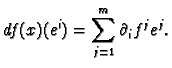Next: The chain rule.
Up: Co-ordinate independent calculus.
Previous: Smooth functions
Contents
Because partial derivatives are co-ordinate dependent
they are not a particularly useful way of thinking about
derivatives if we want to move to a co-ordinate independent
setting such as differentiable manifolds.
It is more useful to think of the derivative
of a function
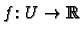 at
at 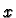 as a linear
map
defined by
We think of this as the rate of change of
as a linear
map
defined by
We think of this as the rate of change of 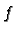 at
at 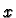 in the
direction of
in the
direction of 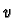 . For smooth functions
. For smooth functions 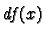 is linear.
Note that
is linear.
Note that 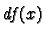 is akin to the notion of a directional derivative
but we do not require that
is akin to the notion of a directional derivative
but we do not require that 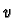 is of unit length. We
can recover the partial derivatives from this definition
by applying the linear operator
is of unit length. We
can recover the partial derivatives from this definition
by applying the linear operator 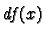 to the vector
to the vector 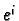 .
The result,
.
The result,
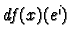 , is just the
, is just the 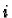 th partial derivative
of
th partial derivative
of 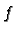 at
at 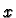 .
.
Similarly if
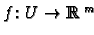 then we define a linear map
then we define a linear map
by
As a linear map we can expand 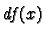 in a basis and we recover
the Jacobian matrix
in a basis and we recover
the Jacobian matrix




Next: The chain rule.
Up: Co-ordinate independent calculus.
Previous: Smooth functions
Contents
Michael Murray
1998-09-16
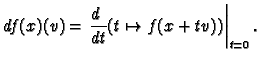
![]() then we define a linear map
then we define a linear map