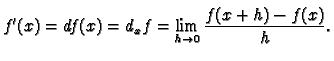Next: Derivatives as linear operators.
Up: Co-ordinate independent calculus.
Previous: Introduction
Contents
Recall that if
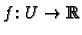 is a function defined
on an open subset
is a function defined
on an open subset 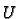 of
of
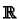 then we say that
then we say that 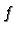 is
differentiable at
is
differentiable at 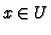 if the limit
if the limit
exists. If the limit exists we call it the
derivative of 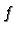 at
at 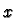 and denote it by any of
and denote it by any of
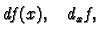
or
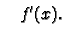
If 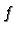 is differentiable at any
is differentiable at any 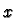 in
in 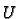 we just say that
we just say that
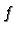 is differentiable.
is differentiable.
If
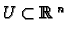 is open and
is open and
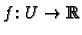 we can define
partial derivatives by varying only one of the co-ordinates.
If
we can define
partial derivatives by varying only one of the co-ordinates.
If 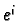 is the element of
is the element of
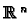 with a
with a 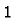 in the
in the 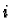 th
position and 0's elsewhere we define a curve by
th
position and 0's elsewhere we define a curve by
The 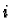 th partial derivative of
th partial derivative of 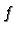 at
at 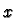 is then defined by
We say that
is then defined by
We say that 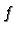 is smooth if it has partial derivative
of any order. Because a differentiable function is continuous
it follows that
is smooth if it has partial derivative
of any order. Because a differentiable function is continuous
it follows that 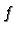 has continuous partial derivative of any
orders. I am quite deliberately avoiding the notation
for the time being.
has continuous partial derivative of any
orders. I am quite deliberately avoiding the notation
for the time being.
If
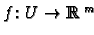 then we say that
then we say that 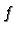 is smooth if
the functions
is smooth if
the functions
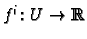 are smooth where
are smooth where
 . Notice
that in this case the limit definition of derivative
makes sense and we can define
. Notice
that in this case the limit definition of derivative
makes sense and we can define




Next: Derivatives as linear operators.
Up: Co-ordinate independent calculus.
Previous: Introduction
Contents
Michael Murray
1998-09-16
![]() is a function defined
on an open subset
is a function defined
on an open subset ![]() of
of
![]() then we say that
then we say that ![]() is
differentiable at
is
differentiable at ![]() if the limit
if the limit
![]() is open and
is open and
![]() we can define
partial derivatives by varying only one of the co-ordinates.
If
we can define
partial derivatives by varying only one of the co-ordinates.
If ![]() is the element of
is the element of
![]() with a
with a ![]() in the
in the ![]() th
position and 0's elsewhere we define a curve by
th
position and 0's elsewhere we define a curve by
![]() then we say that
then we say that ![]() is smooth if
the functions
is smooth if
the functions
![]() are smooth where
are smooth where
![]() . Notice
that in this case the limit definition of derivative
makes sense and we can define
. Notice
that in this case the limit definition of derivative
makes sense and we can define