



Next: Integration again
Up: Differential forms.
Previous: Integration of differential forms
Contents
Let 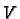 be a real vector space of
dimension
be a real vector space of
dimension 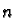 . Then define
. Then define
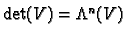 .
This is a real, one dimensional vector space.
So the set
.
This is a real, one dimensional vector space.
So the set
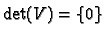 is disconnected.
An orientation of the vector space
is disconnected.
An orientation of the vector space 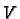 is a choice
of one of these connected components.
If
is a choice
of one of these connected components.
If 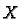 is an invertible linear map from
is an invertible linear map from 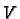 to
to 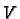 then it induces a linear map from
then it induces a linear map from
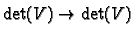 which is therefore multiplication by a complex number.
This number is just
which is therefore multiplication by a complex number.
This number is just 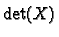 the determinant of
the determinant of 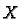 If
If 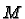 is a manifold of dimension
is a manifold of dimension 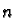 then the same
applies to
then the same
applies to 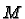 ;
;
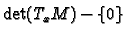 is a disconnected set.
We define
is a disconnected set.
We define
Definition 5.2
A manifold is orientable if there is a non-vanishing
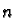
-form on
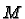
. Otherwise it is called non-orientable.
If 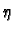 and
and 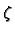 are two non-vanishing
are two non-vanishing
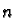 forms then
forms then
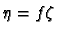 for some
function
for some
function 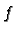 which is either strictly negative
or strictly positive. Hence the set of
non-vanishing
which is either strictly negative
or strictly positive. Hence the set of
non-vanishing 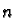 forms divides into two sets. We
have
forms divides into two sets. We
have
Definition 5.3 (Orientation)
An orientation on
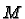
is a choice of one of these two sets.
An orientation defines an orientation on each
tangent space 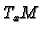 . We call an
. We call an 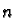 form positive
if it coincides with the chosen orientation negative
otherwise. We say a chart
form positive
if it coincides with the chosen orientation negative
otherwise. We say a chart 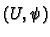 is
positive or oriented if
is
positive or oriented if
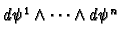 is positive. Note that if a chart is not positive we
can make it so by changing the sign of one co-ordinate function
so oriented charts exits. If we chose two oriented charts
then we have that
is positive. Note that if a chart is not positive we
can make it so by changing the sign of one co-ordinate function
so oriented charts exits. If we chose two oriented charts
then we have that
is an oriented diffeomorphism. The converse is also
true.
Proposition 5.6
Assume we have a covering of
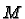
by co-ordinate
charts
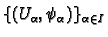
such that for any
two
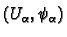
and
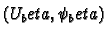
the diffeomorphism
is orientation preserving. Then there is an orientation
of
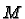
which makes each all these charts
oriented.
Proof.
Notice that the fact that
is an oriented diffeomorphism means that if
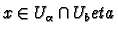
then
is a positive multiple of
Hence if
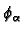
is a partition of unity then
is a non-vanishing
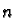
form. Clearly this defines the
required orientation.





Next: Integration again
Up: Differential forms.
Previous: Integration of differential forms
Contents
Michael Murray
1998-09-16
![]() and
and ![]() are two non-vanishing
are two non-vanishing
![]() forms then
forms then
![]() for some
function
for some
function ![]() which is either strictly negative
or strictly positive. Hence the set of
non-vanishing
which is either strictly negative
or strictly positive. Hence the set of
non-vanishing ![]() forms divides into two sets. We
have
forms divides into two sets. We
have
![]() . We call an
. We call an ![]() form positive
if it coincides with the chosen orientation negative
otherwise. We say a chart
form positive
if it coincides with the chosen orientation negative
otherwise. We say a chart ![]() is
positive or oriented if
is
positive or oriented if
![]() is positive. Note that if a chart is not positive we
can make it so by changing the sign of one co-ordinate function
so oriented charts exits. If we chose two oriented charts
then we have that
is positive. Note that if a chart is not positive we
can make it so by changing the sign of one co-ordinate function
so oriented charts exits. If we chose two oriented charts
then we have that