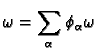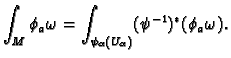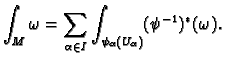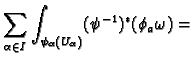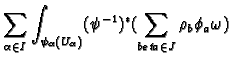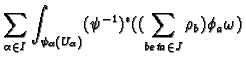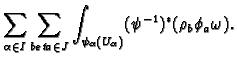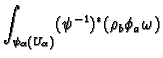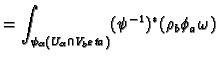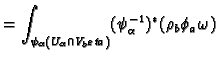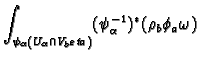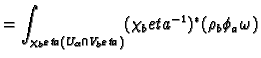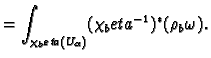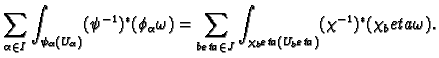Next: Orientation.
Up: Differential forms.
Previous: Pulling back differential forms
Contents
Let
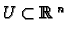 and
and
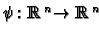 be a diffeomorphism.
Then it is well known that if
be a diffeomorphism.
Then it is well known that if
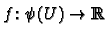 is
a function then
is
a function then
In this formula we regard
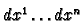 as the symbol for
Lebesgue measure. However it is very suggestive of
the notation for differential forms developed in the previous
section.
as the symbol for
Lebesgue measure. However it is very suggestive of
the notation for differential forms developed in the previous
section.
If 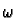 is a differential
is a differential 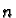 form on
form on
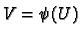 then we can write it as
then we can write it as
If we pull it back with the diffeomorphism 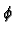 then,
as we seen before,
So differential
then,
as we seen before,
So differential 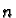 forms transform by the determinant
of the jacobian of the diffeomorphism and Lebesgue measure transforms
by the absolute value of the determinant of the
jacobian of the diffeomorphism. We define the integral of
a differential
forms transform by the determinant
of the jacobian of the diffeomorphism and Lebesgue measure transforms
by the absolute value of the determinant of the
jacobian of the diffeomorphism. We define the integral of
a differential 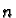 form by
when
form by
when
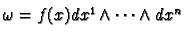 .
Alternatively we can write this as
Call a diffeomorphism
.
Alternatively we can write this as
Call a diffeomorphism
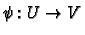 orientation preserving if
for all
orientation preserving if
for all 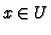 . Then we have
. Then we have
Proposition 5.5
If
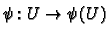
is an orientation preserving
diffeomorphism and
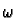
is a differential
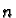
form
on
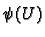
then
We can use this proposition to define the integral of
differential forms on a manifold. Let
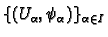 be a covering of
be a covering of 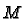 by co-ordinate charts. Choose a
partition of unity
by co-ordinate charts. Choose a
partition of unity
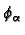 subordinate to
subordinate to 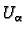 . Then
if
. Then
if 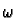 is a differential
is a differential 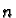 form we can write
form we can write
where the support of
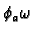 is
in
is
in 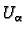 . First we define the integral
of each of the forms
. First we define the integral
of each of the forms
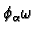 Then we define the integral of
Then we define the integral of 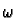 to be
We have to show that this is independent of all the choices
we have made. So let us take another open cover
to be
We have to show that this is independent of all the choices
we have made. So let us take another open cover
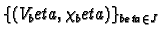 with partition of unity
with partition of unity
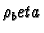 . Then we have
. Then we have
The differential forms
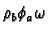 have support in
have support in
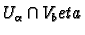 so we have
so we have
If the diffeomorphism
is orientation preserving then we have
So we can complete the calculation above and have
All this calculation rests on the fact that
is an orientation preserving diffeomorphism. In
general this will not be the case. We have to
introduce the notion of an oriented manifold and
and oriented co-ordinate chart. Before we can do
that we need to discuss orientations on a vector
space.




Next: Orientation.
Up: Differential forms.
Previous: Pulling back differential forms
Contents
Michael Murray
1998-09-16
![]() and
and
![]() be a diffeomorphism.
Then it is well known that if
be a diffeomorphism.
Then it is well known that if
![]() is
a function then
is
a function then
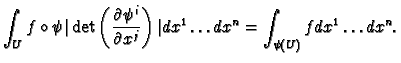
![]() is a differential
is a differential ![]() form on
form on
![]() then we can write it as
then we can write it as
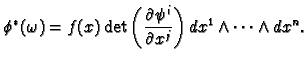
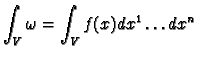
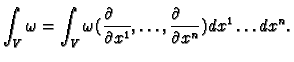
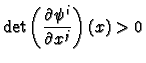
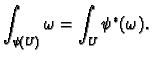
![]() be a covering of
be a covering of ![]() by co-ordinate charts. Choose a
partition of unity
by co-ordinate charts. Choose a
partition of unity
![]() subordinate to
subordinate to ![]() . Then
if
. Then
if ![]() is a differential
is a differential ![]() form we can write
form we can write