



Next: Vector fields.
Up: The tangent space.
Previous: The tangent to a
Contents
If 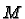 is a manifold then we can define a
submanifold of
is a manifold then we can define a
submanifold of 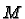 by using the
principal property of submanifolds in
by using the
principal property of submanifolds in
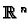 .
.
Definition 4.4 (Submanifolds.)
We say that a subset
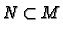
is a submanifold
of dimension
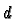
of a manifold
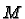
of dimension
if for every
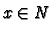
we can
find a co-ordinate chart
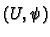
for
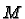
with
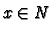
and such that
Just as before we can define co-ordinates
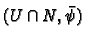 on
on
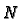 by letting
by letting
for each
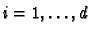 . Similarly we have
. Similarly we have
Proposition 4.4
The set consisting of all the charts
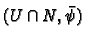
constructed in this manner is an atlas. Moreover it makes
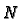
a manifold in such a way that the inclusion map
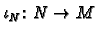
defined by
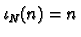
is smooth.
Because the condition for being a submanifold is local we can
use the inverse function theorem as in Proposition
4.2 to prove
Proposition 4.5
Let
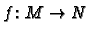
be a smooth map
between manifolds of dimension
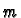
and
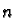
respectively.
Let
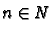
and
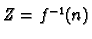
. Then if
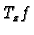
is onto for all
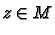
the set
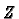
is
submanifold of
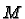
. Moreover the image of
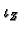
in
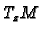
is precisely the kernel of
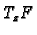
.




Next: Vector fields.
Up: The tangent space.
Previous: The tangent to a
Contents
Michael Murray
1998-09-16
![]() on
on
![]() by letting
by letting