-
Linear Algebra for the 21st Century
This textbook provides an forward-looking introduction and
development of the power of linear algebra in modern
science, engineering and computing. It is designed with
established learning principles. Published by Oxford
University Press.
Linear Algebra for the 21st Century will be an excellent basis for an introductory course in linear algebra (Joakim Sundnes, 2022)
- The best LaTeX introduction shows how to transform plain text into a beautifully typeset document in LaTeX. It introduces what many consider are the most important fundamentals of LaTeX2e. See youtube playlist.
-
Modelling emergence
Compile your own tailored version of my book to learn modern
methods of modelling complex dynamical systems.
Maurício Kritz (2019) commented in reference to the book:
develops methods, techniques, and algorithms for studying the behaviour of systems ... necessity of having simple models, equations and mathematics as brilliantly explained ... the huge and beautiful knowledge accumulated recently about dynamical systems.
- Holistic discretisation of dynamical Partial Differential Equations obtain the spatial discretisation of one or three coupled dynamical PDEs using dynamical systems theory. It is a now well-established, mathematically sound, algebraically reliable, approach analogous to the current trendy machine-learning/neural-network/artificial-intelligence ad hoc approaches to spatial discretisations.
-
SDE slow manifold et
al. constructs for you the the slow manifold of any
supplied stochastic differential equations (SDEs), or
deterministic non-autonomous ODEs, when the DEs have slow
modes and fast stable/unstable modes. The slow manifold
model supplies you with a faithful large time model of the
stochastic dynamics.
The "et al." indicates that you can ask for any other common (stochastic) invariant manifold of your supplied SDEs or deterministic non-autonomous ODEs. You can also ask for a normal form of the entire state space which decouples the various invariant manifolds.
-
Construct invariant manifolds
constructs for you a specified invariant manifold and
evolution thereon of your specified system of
autonomous ordinary differential equations (ODEs).
It applies to pitchfork or Hopf bifurcations or higher order
degeneracies. The invariant manifold you request may be a
centre manifold, a slow manifold, a stable manifold, a
spectral submanifold, etc. The analysis transforms one or
coupled oscillators into modulation equations to replace
averaging and homogenisation.
From 2014 added code to compute, in the case of a slow manifold, a basis of normal vectors to the isochrons in order to model initial conditions, non-autonomous forcing, and uncertainty quantification.
- Multifractal analyser estimation of fractal dimensions, let alone multifractal dimensions, are fraught with subtle difficulties. Use this state of the art service to estimate fractal dimensions for your 1D, 2D or 3D datasets.
- Construct lego fractals to stun your friends.
- List of research and teaching publications with links to many electronic versions.
- Two youtube playlists contain videos of some selected topics and examples:
Climate change?
The atmosphere is like the 'tail of the dog': it is hard to see where the climate 'dog' is going from the 'wagging tail' of the atmosphere's temperature. The ocean has a heat capacity a thousand times that of the atmosphere, and takes hundreds of years to warm and/or cool---the ocean is like the 'body of the dog' of climate. So instead of looking at atmospheric temperatures, look to the ocean to see where the climate is going. As the ocean warms, it expands, and so sea level rises. As glaciers increasingly melt, the sea level rises. The following graph indicates where the ocean is going [thanks to the CSIRO at https://www.cmar.csiro.au/sealevel/sl_hist_last_decades.html ]: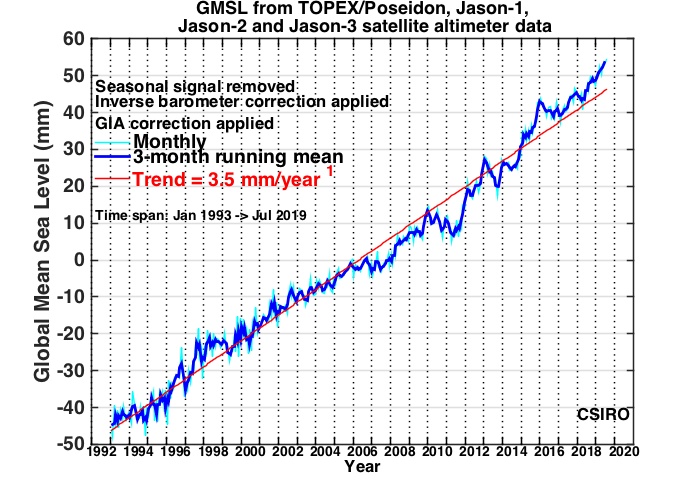
Erdos number 3
The Erdos Number is the distance from Paul Erdos (1913--1996) on a graph whose edges denote the relationship of coauthorship in scientific articles [ http://www.oakland.edu/enp]:- Pollett, P. K.; Roberts, A. J. A description of the long-term behaviour of absorbing continuous-time Markov chains using a centre manifold. Adv. in Appl. Probab. 22 (1990), 111--128.
- Brown, T. C.; Pollett, P. K. Some distributional approximations in Markovian queueing networks. Adv. in Appl. Probab. 14 (1982), 654--671.
- Brown, T. C.; Erdos, P.; Chung, F. R. K.; Graham, R. L. Quantitative forms of a theorem of Hilbert. J. Combin. Theory Ser. A 38 (1985), 210--216.
If you like this web page, please link to it so others can find it more easily.