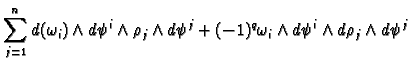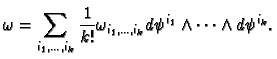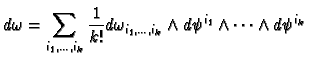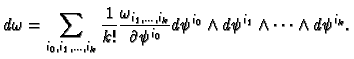Definition 5.1 (Differential form.)
A differential form
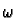
is smooth if its components with respect to a
collection of co-ordinate charts whose domains cover
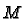
are smooth.
Proof.
We define
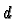
recursively. We have the
ordinary definition of
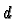
if
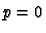
. We assume that
we have it defined for all
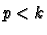
and that
the conditions (i), (ii) and (iii) hold when ever they
make sense. Consider a
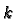
form
.
Let
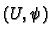
be a co-ordinate chart and let
Then define
so that
Notice that
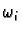
is uniquely defined by
this equation because
Consider now another choice of co-ordinates
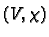
. We have
where
It is easy to check that on 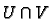 we have
we have
Then if the proposition is to be true we must have
This defines a differential
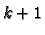
form on the open
set
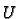
. On the open set

it is defined by
and we need to check that these two agree.
We have
Hence
The first term vanishes because the partial
derivative is symmetric in
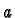
and
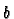
and the
wedge product is anti-symmetric. Hence we have
as required.
Clearly condition (i) is still true. For (ii) note
that
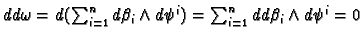
.
For the final condition let
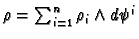
.
Assume that
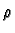
has degree
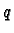
. Then
so that
Then applying the result for degrees lower than
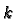
we have
Putting this altogether we have
as required.

Example 5.2
Recall from
5.1 the way in which we identified
one-forms and two-forms on
with vectors. It follows
that differentiable one and two forms on
can be
identified with vector-fields. Similarly zero and
three forms are functions. With these identifications
it is straightforward to check that the exterior
derivative of zero, one and two forms corresponds
to the classical differential operators grad, curl and div.
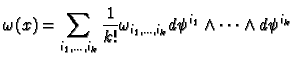
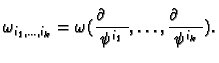
![]() the set of all
smooth differentiable
the set of all
smooth differentiable ![]() forms on
forms on ![]() . Notice that
. Notice that
![]() is just
is just
![]() the space of all smooth
functions on
the space of all smooth
functions on ![]() .
.
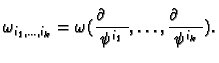
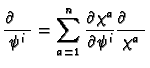
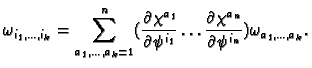
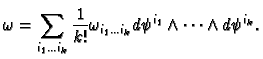
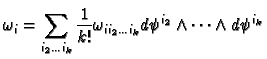
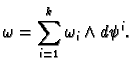
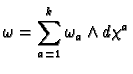
![]() we have
we have
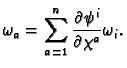
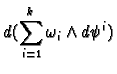
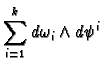
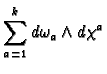
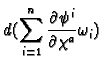
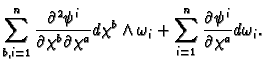
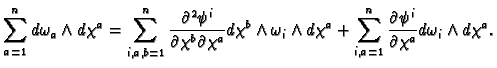
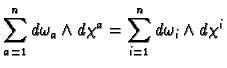
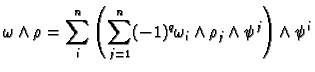
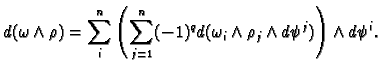
![$\displaystyle \sum_{j=1}^n \left[(-1)^q d(\omega_i)\wedge \rho_j \wedge d\psi^j + (-1)^{p+ q-1} \omega_i \wedge d\rho_j \wedge d\psi^j\right] \wedge d\psi^i$](img598.gif)