



Next: Differential forms and the
Up: Differential forms.
Previous: Differential forms.
Contents
If  is a vector space we define a
is a vector space we define a 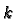 -linear
map to be a map
where there are
-linear
map to be a map
where there are 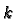 copies of
copies of  , which is linear
in each factor. That is
, which is linear
in each factor. That is
We define
a 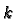 -linear map
-linear map 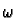 to be totally antisymmetric if
for all vectors
to be totally antisymmetric if
for all vectors
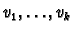 and all
and all 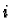 .
Note that it follows that
and if
.
Note that it follows that
and if
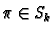 is a permutation of
is a permutation of
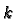 letters then
letters then
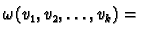
sgn
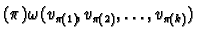
where
sgn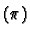 is the sign of the permutation
is the sign of the permutation 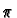 . We denote the
vector space of all
. We denote the
vector space of all 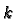 -linear, totally antisymmetric maps by
-linear, totally antisymmetric maps by
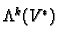 . and call them
. and call them 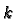 forms. If
forms. If 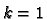 the
the
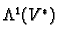 is just
is just 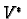 the space of all linear functions on
the space of all linear functions on  and if
and if 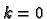 we make the convention that
we make the convention that
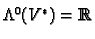 . We need to
collect some results on the linear algebra of these spaces.
. We need to
collect some results on the linear algebra of these spaces.
Assume that  has dimension
has dimension 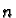 and that
and that
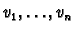 is a basis
of
is a basis
of  . Let
. Let 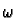 be a
be a 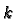 form. Then if
form. Then if
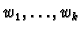 are arbitrary vectors and we
expand them in the basis as
are arbitrary vectors and we
expand them in the basis as
then we have
so that it follows that 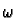 is completely determined by
its values on basis vectors. In particular if
is completely determined by
its values on basis vectors. In particular if 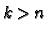 then
then
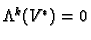 .
.
If 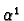 and
and 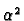 are two linear maps in
are two linear maps in 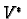 then we
define an element
then we
define an element
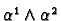 ,
called the wedge product of
,
called the wedge product of 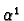 and
and 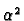 , in
, in
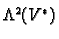 by
by
More generally if
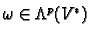 and
and
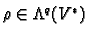 we define
we define
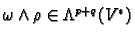 by
by
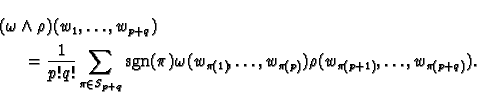
Assume that
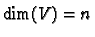 . Then we leave as an exercise the following proposition.
. Then we leave as an exercise the following proposition.
Proposition 5.1
The direct sum
with the wedge product is an associative algebra.
We call
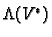 the exterior
algebra of
the exterior
algebra of 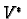 . We call an element
. We call an element
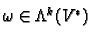 an element of degree
an element of degree 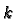 .
Because of associativity we can
repeatedly wedge and disregard brackets.
In particular we can define the wedge product of
.
Because of associativity we can
repeatedly wedge and disregard brackets.
In particular we can define the wedge product of 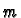 elements in
elements in 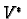 and we leave it as an exercise to show that
and we leave it as an exercise to show that
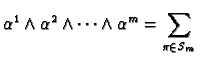
sgn
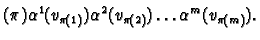
Notice that
and that
Still assuming that  is
is 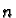 dimensional
choose a basis
dimensional
choose a basis
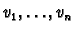 of
of  .
Define the dual basis of
.
Define the dual basis of 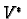 ,
,
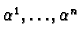 ,
by
,
by
for all 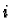 and
and 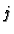 . We want to define a basis of
. We want to define a basis of
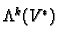 .
Define elements of
.
Define elements of
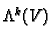 by choosing
by choosing 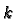 numbers
numbers
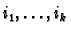 between
between 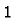 and
and 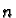 and
considering
As we are trying to form a basis
we may as well keep
the
and
considering
As we are trying to form a basis
we may as well keep
the 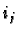 distinct and ordered
distinct and ordered
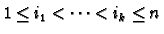 . We show first
that these elements span
. We show first
that these elements span
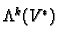 . Let
. Let 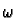 be an element of
be an element of
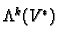 . Notice that
equals zero unless there is a permutation
. Notice that
equals zero unless there is a permutation 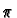 such that
such that
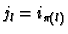 for all
for all 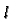 and equals
sgn
and equals
sgn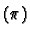 if
there is such a permutation. Consider vectors
if
there is such a permutation. Consider vectors
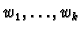 and expand them in the basis as
Then we have
so that it follows that
and expand them in the basis as
Then we have
so that it follows that 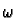 is completely determined by
its values on basis vectors. For any ordered
is completely determined by
its values on basis vectors. For any ordered 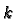 -tuple
-tuple
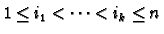 define
and consider
We show that
define
and consider
We show that
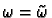 . It suffices to apply both sides to
vectors
. It suffices to apply both sides to
vectors
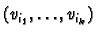 for any
for any
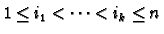 and show that they are equal but that
is clear from previous discussions. So
and show that they are equal but that
is clear from previous discussions. So
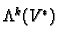 is
spanned by the basis vectors
is
spanned by the basis vectors
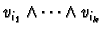 .
We have
.
We have
Proposition 5.2
The vectors
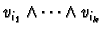
where
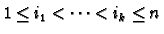
are a basis for
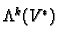
.
Proof.
We have already seen that these vectors span. It suffices to
show that they are linearly independent. We do this by induction
on
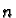
. If
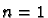
then the result is clear as the only non-trivial
case is
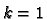
when the result is straightforward. More generally
assume we have a linear relation amongst some of the
basis vectors. There has to be an index
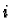
such that the corresponding
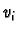
does not occur in all the vectors in that linear relation.
Otherwise there is only one vector in the linear relation and that
is not possible. Then wedge the whole relation with
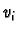
. The
terms containing
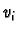
disappear and we obtain a relation between
the vectors constructed for the case of a dimension less so by
induction that is not possible.

It is sometimes useful to sum over all 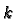 -tuples
-tuples
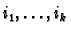 not just ordered ones. We can do this -- an
keep the uniqueness of the coefficients
not just ordered ones. We can do this -- an
keep the uniqueness of the coefficients
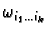 --
if we demand that they be antisymmetric. That is
--
if we demand that they be antisymmetric. That is
Then we have
We will need one last piece of linear algebra called contraction.
Let
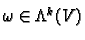 and
and  . Then we define
a
. Then we define
a 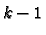 form
form
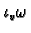 , the contraction of
, the contraction of
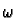 and
and 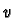 by
by
where
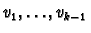 are any
are any 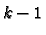 elements of
elements of
 .
.
Example 5.1
Consider the vector space
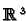
. Then we know that
zero forms and one forms are just real numbers and
linear maps respectively. Notice that in the case
of
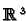
we can identify any linear map
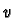
with
the vector
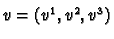
where
Let 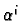 be the basis of linear functions defined
by
be the basis of linear functions defined
by
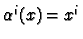 . We have seen that every two
form
. We have seen that every two
form 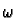 on
on
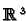 has the form
has the form
Every three-form
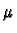
takes the form
It follows that in
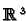 we can identify three-forms
with real numbers by identifying
we can identify three-forms
with real numbers by identifying 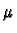 with
with
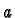 and we can identify two-forms with vectors
by identifying
and we can identify two-forms with vectors
by identifying 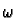 with
with
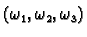 .
.
It is easy to check that with these identifications
the wedge product of two vectors 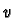 and
and 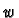 is identified
with the vector
is identified
with the vector
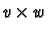 . In other words wedge
product corresponds to cross product.
. In other words wedge
product corresponds to cross product.




Next: Differential forms and the
Up: Differential forms.
Previous: Differential forms.
Contents
Michael Murray
1998-09-16
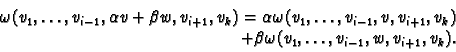
![]() has dimension
has dimension ![]() and that
and that
![]() is a basis
of
is a basis
of ![]() . Let
. Let ![]() be a
be a ![]() form. Then if
form. Then if
![]() are arbitrary vectors and we
expand them in the basis as
are arbitrary vectors and we
expand them in the basis as
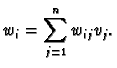
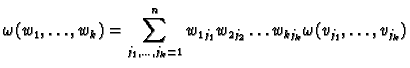
![]() and
and ![]() are two linear maps in
are two linear maps in ![]() then we
define an element
then we
define an element
![]() ,
called the wedge product of
,
called the wedge product of ![]() and
and ![]() , in
, in
![]() by
by
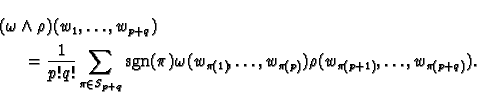
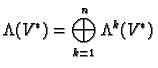
![]() the exterior
algebra of
the exterior
algebra of ![]() . We call an element
. We call an element
![]() an element of degree
an element of degree ![]() .
Because of associativity we can
repeatedly wedge and disregard brackets.
In particular we can define the wedge product of
.
Because of associativity we can
repeatedly wedge and disregard brackets.
In particular we can define the wedge product of ![]() elements in
elements in ![]() and we leave it as an exercise to show that
and we leave it as an exercise to show that
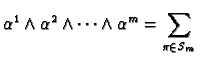 sgn
sgn![]() is
is ![]() dimensional
choose a basis
dimensional
choose a basis
![]() of
of ![]() .
Define the dual basis of
.
Define the dual basis of ![]() ,
,
![]() ,
by
,
by
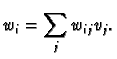
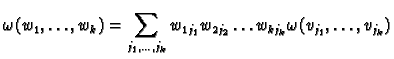
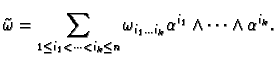
![]() -tuples
-tuples
![]() not just ordered ones. We can do this -- an
keep the uniqueness of the coefficients
not just ordered ones. We can do this -- an
keep the uniqueness of the coefficients
![]() --
if we demand that they be antisymmetric. That is
--
if we demand that they be antisymmetric. That is
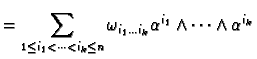
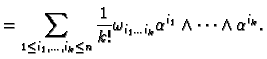
![]() and
and ![]() . Then we define
a
. Then we define
a ![]() form
form
![]() , the contraction of
, the contraction of
![]() and
and ![]() by
by
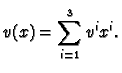
![]() be the basis of linear functions defined
by
be the basis of linear functions defined
by
![]() . We have seen that every two
form
. We have seen that every two
form ![]() on
on
![]() has the form
has the form
![]() we can identify three-forms
with real numbers by identifying
we can identify three-forms
with real numbers by identifying ![]() with
with
![]() and we can identify two-forms with vectors
by identifying
and we can identify two-forms with vectors
by identifying ![]() with
with
![]() .
.
![]() and
and ![]() is identified
with the vector
is identified
with the vector
![]() . In other words wedge
product corresponds to cross product.
. In other words wedge
product corresponds to cross product.