



Next: Differential forms.
Up: The tangent space.
Previous: Vector fields.
Contents
One use of this discussion is the
definition of the Lie bracket of two vector
fields. Let 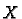 and
and 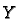 be two vector
fields and write them locally as
and
so that
be two vector
fields and write them locally as
and
so that
Then define
We leave it as an exercise to show that this
transforms as a vector field. We call ![$ [X, Y]$](img470.gif) the
Lie bracket of the vector fields
the
Lie bracket of the vector fields 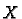 and
and 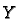 .
Lie is named after Sophus Lie and pronounced "lee".
.
Lie is named after Sophus Lie and pronounced "lee".
Michael Murray
1998-09-16
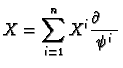
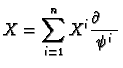
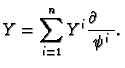
![$\displaystyle [X, Y] = \sum_{i, j=1}^n (X^j\frac{\partial Y^i}{\partial \psi^j}...
...\frac{\partial X^i}{\partial \psi^j}) \frac{\partial\phantom{\psi^i}}{\psi^i}.
$](img469.gif)